■この記事のターゲット
・品質保証部って最低限どんなスキルがあればいいの?
・正規分布と工程能力指数をどうやって品質管理に使っていけばいいの?
今回の記事は、品質管理に最低限必要なスキル「正規分布」と「工程能力指数」について述べてみたいと思います。
みなさんも聞いたこともあると思いますし、実際活用している方も多いでしょう。
確率・統計に絡む話ですね。
これらは製造業の品質保証の仕事をされている方に最低限必要なスキルであると同時に、ぶっちゃけこの二つをしっかり理解しておけば大体の計量データを分析できます。そして、次の行動のための判断材料にすることができます。
当然、 「正規分布」と「工程能力指数」を語るために付随する
・最小値(あるデータの集まりの中の最も小さい値)
・最大値 (あるデータの集まりの中の最も大きい値)
・平均値 (あるデータの集まりの中の平均的な値)
・分散 (あるデータの集まりの中のデータのバラツキ度合い)
・標準偏差(分散計算値と元データとの単位を合わせることでバラツキ度合いを分かりやすくしたもの)
も理解しておく必要がありますが、そんなものは屁でもないでしょう。
標準偏差はちょっと分かりにくいかもしれませんが、データの集まり(集団)のバラツキ度合い (平均値からかけ離れたデータ数が多いか少ないか) を表す数値という理解でいいです。
表計算ソフトの関数(Excelで言えば STDEV)で計算させればサクッと算出できますので意味だけ知っておけば問題なし!
今までは感覚で判断していたような事柄を、計量データを取って正規分布や工程能力指数で数値的に肉付けできると非常に信ぴょう性が高くなるという便利なモノです。
正規分布について深く知ろうと思うと聞き慣れない用語がたくさん出てきて頭が混乱します(笑)
我々は研究者や数学者じゃないので、単純に使い方だけを知ればいいんですよ。
ということで、学術的な表現はなるべく使わないようにして感覚的に分かるように述べたいと思います。
さあ、あなたも正規分布&工程能力指数をカジュアルに使いこなしましょう!
正規分布について
あるデータ、例えば切削加工設備で加工した製品の寸法Aのデータが100個あるとしましょう。
その寸法はある範囲内でバラついています。
その寸法Aのデータ20個の度数分布(例:9.5mmのデータが1個、10mmのデータが4個、…10.5mmのデータが1個)を表にして、ヒストグラムを作るとこんな感じになります。
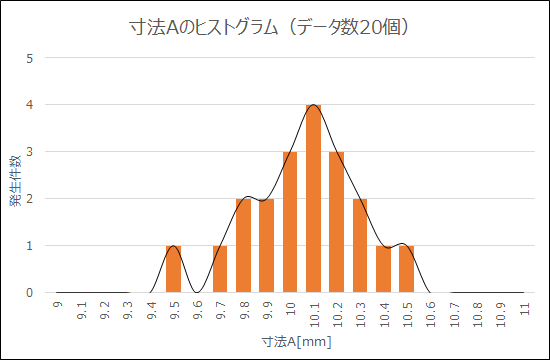
各データ範囲の発生頻度の頂点を結ぶと、おおよそ「釣り鐘状」の形状(と、あえて言い切ります(笑))となります。
このように釣り鐘状に発生頻度が分布していることを一般的に「寸法Aのデータ発生頻度は正規分布に従っている」とみなします。
例外もあるのですが、製造業で管理するような狙い値が存在するデータの発生頻度などは世間一般的に正規分布に従うと言われています。
正規分布は、データの集まり(集団)の平均値とバラツキの度合いをしめす標準偏差をパラメーターに持つ確率密度関数なのです。
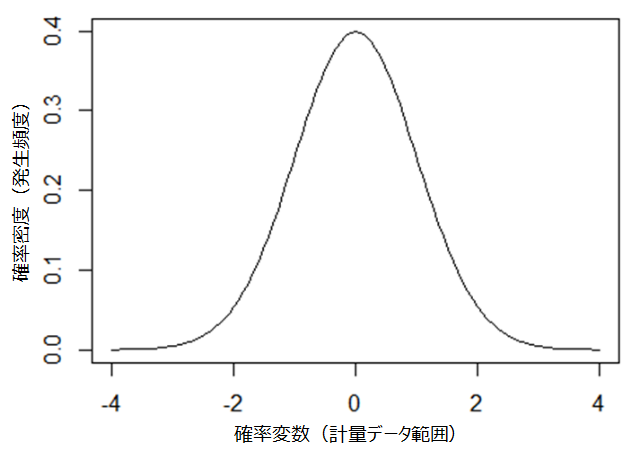
学問的には平均値がゼロで標準偏差が1の「標準正規分布」の確率分布カーブは下図のようになります。
一般的に「正規分布に従う」ということは、確率変数(上記例では寸法Aの計量値)は下図のカーブのような発生頻度になると仮定するということです。
釣り鐘形状にちなんで 「bell curve(ベル・カーブ)」とも呼ばれます。
ちなみに確率変数はー∞~+∞であり、 ー∞~+∞ の範囲の確率密度カーブの面積は1になります。言い換えるとデータ範囲すべての発生頻度の合計は100%ということになります。
つまり、この関数に基づくことでデータの発生確率予測ができるということです。
正規分布を知ることでできること
正規分布は、あるデータの出現確率を求めるための関数です。
つまり、あるデータの発生確率が正規分布に従うと仮定すれば、ある程度の大きさのデータ集団の平均値(Ave)と標準偏差(σ)が分かれば「今後のデータの発生頻度確率を予測できる」ということです。
そして、データの数が多ければ多いほど精度の高い予測ができる (中心極限定理 と言います)という大変便利な考え方になってます。
※中心極限定理…簡単に言うとデータ数が大きくなればなるほど標準正規分布の形状に近づいていくこと
正規分布を活用したデータ分布の分析方法
正規分布関数を使って実際にデータ予測をする時によく使われるのが以下の2つの方法です。
①正規分布表を使った特定の数値データの出現確率予測
②一般的なデータの管理上限と下限値を決める判断材料とする
2つと言いつつも、厳密に言えば原理は一緒なので見せ方が違うだけなのですが、あえて分かりやすく2つと言っておきます(笑)
①正規分布表を使った特定の数値データの出現確率予測
前述の製品の寸法Aのデータを例にとって説明します。
寸法Aが10.2以上となる確率を求めてみましょう。
標準正規分布表(後で述べます)とデータの平均値(Ave)、標準偏差(σ)があれば、任意のデータ範囲の発生頻度予測が可能です。
まず、10.2の寸法Aのデータを標準化します。
標準化とは、標準正規分布の考え方に乗せるための変換みたいなものです。

ここで、計算に必要なデータは以下のようになります。
平均値Ave:10.00
標準偏差σ:0.26
よって、標準化を行うとz=0.78となります。
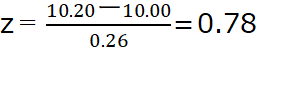
ここで冒頭で述べた「標準正規分布表」の登場です!
標準正規分布表とはzから確率を求めるための表で、決まりきったものです。
学校で確率・統計を習った人はご存じと思います。
一部抜粋すると、こんな表です。ググればすぐに出てくるので見てみてください。
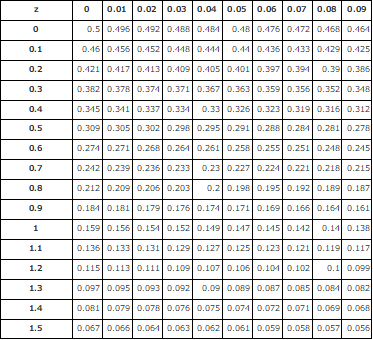
先ほど求めたzに対応する値を正規分布表から探します。
今回の例で言えば、0.218になります。
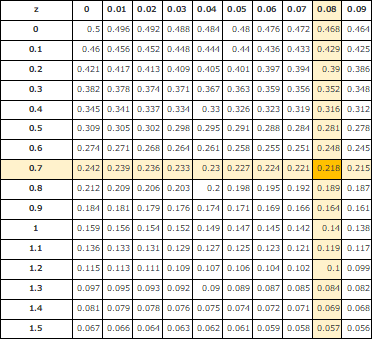
この0.218から何が言えるかというと「寸法Aが10.2以上になる確率が21.8%」ということです。
なお、10.2より小さい確率は100%ー21.8%で78.2%とも言えます。
場合によってはzが負の数(例えば-0.78)となることもありますが、表を見るときは絶対値をとりますのでマイナスを無視して表から値を取ればいいです。
もっと詳しく知りたい方は、Bell Curveというサイトをご覧ください。
いろいろと統計について勉強できますよ!
Bell Curve 統計WEBへのリンク
②一般的なデータの管理上限と下限値を決める判断材料とする
これは過去からよく使われている「簡易的にデータの分布感を知る方法」です。
求め方は簡単。「平均値±3σ」だけ。
この式で求められた2つの値の範囲内にデータの99.7%が含まれるという意味になります。
(言い換えると、「0.3%の確率で範囲外」となる)
寸法Aの例では、
Ave+3σ=10.78
Ave-3σ=9.21
となります。
この数値を基にデータのばらつき具合を判断し、検査規格値を決めたり加工精度を高めたりの判断をするわけです。
もちろん、ここで数式をAve±4σとしても問題ありません。4σの場合は2つの値の範囲内にデータの99.94%が含まれるという意味になります。
次の項で述べる工程能力指数とも関連してきますので、あわせて読み進めてもらえるとよいかと。
工程能力指数について
続いて工程能力指数(Cpk)についてです。
分かりやすく、製造業のある加工プロセス上の管理値で説明します。
ある工程で加工した寸法Xを検査工程で測定器で測定し、合格不合格を判定するものとします。そして、設計指示(検査規格)が10±1mmであったとしましょう。
つまり、規格上限値は11mmで規格下限値は9mmということになります。
当然、加工工程では寸法Xが9~11mmの間にキッチリ収まるように加工しなければいけません。
工程能力指数は、
加工工程で作り出される寸法Xの確率分布が正規分布に従うとして、そのデータ分布が管理上限11mmと管理下限9mmに対してどのような関係を持つか、つまり加工工程の加工実力は規格値に対してどういうレベルかを数値的に判断しやすくする指標です。
言い換えると、正規分布に規格値上下限の概念を加えて加工工程の加工精度実力を数値として表すためのものになります。
工程能力指数を活用してできること
工程能力指数は0以上の数字で表現されます。
工程能力指数は1.0が普通レベルであり、一般的に1.33以上あれば規格値に対して十分余裕を持った「加工の能力」を持っているというような判断をすることが多いです。
文字通り、ある工程の能力を数値化するということですが、この指数により
・工程能力指数が低い=規格外れを起こしやすい状態 ⇒ 何らかの施策で加工実力を上げなければならない or 規格値の設定が厳しすぎる
・工程能力指数が極めて高い=ほぼ規格外れが起こることは無い ⇒ 能力過剰なので、加工精度を多少犠牲にしてコストを下げる施策が打てないか or 規格値が緩すぎる
と言った判断が数値に基づいてできるようになるのです。
工程能力指数の求め方
では、工程能力指数の求め方です。
小難しく書いてるようにも見えますが、Excelなどで計算式を埋め込んでおけばイチイチ計算式を意識しておく必要なんてないですよ!

上の式のように計算に必要なものは以下になるので、そこまでの準備はマジメにやりましょう。
・工程能力指数で表したい生データ(多ければ多いほどいいですが、最低30データ以上は欲しい)
・そのデータの規格上限値と下限値
・集めた生データの平均値
・集めた生データの標準偏差
前述の式のように、工程能力指数の求め方は「規格値と平均離れ具合」を「標準偏差の3倍で割る(÷3σ)」という行為です。
正規分布の項でも述べましたが、±3σ(さんシグマ)を使って「99.7%の確率で発生するデータの範囲」を予測することができます。
工程能力指数Cpk=1.0ということは、その工程で作り出す管理値は「規格に対して99.7%の確率で合格」という意味です。
そしてCpk=1.33というのは、その工程で作り出す管理値が 「規格に対して99.94%の確率(±4σ)で合格」するということになり、つまり10,000個に6個の規格外れが出る「工程の実力」だという事です。
工程能力指数からどう判断するか
気を付けて欲しいのは、工程能力指数Cpkが「1だから悪い」とか「1.33だから良い」という単純な議論にならないように気を付けましょう。
業種、会社の方針、コストなど様々な背景を加味して各自が「工程能力指数」からどう考えるかが最も重要なのです。
例えば、ある業種では0.3%の不良 (±3σ) が発生する状況でも、お客様影響やコストのバランスを考えると問題なしと判断するケースもあっていいと思います。
一方、ある業種では0.06%の不良 (±4σ)が発生する状況でも、お客様影響が重大と判断するケースもあるのです。
特に人命などに関わる重要なパラメーターであれば、10,000分の1であろうと低い確率とはみなさないでしょう。
「工程能力指数の数値から何かを判断したい人の環境」と工程能力指数を各自で重みづけしなければならないということです。
数値はしょせん単なる数値でしかありません。
「ある意味」を含んだ数値に基づき行動を判断するのは結局人間なので、会社などであれば品質に対する組織全体の行動方針が重要になってくるというわけです。
工程能力指数Cpkをどう活用していくかについて、別の記事でもう少し詳しく説明しています。
正規分布と工程能力指数まとめ
それではまとめます。
・正規分布は確率密度関数だよ!
・繰り返し作業などで生み出される数値データの発生予測ができるよ!
・生データと平均値、標準偏差、正規分布表があればいいよ!
・平均値±3σ(シグマ)の考えは身に付けておいて損はないよ!
・正規分布がベースだよ!
・あるプロセスが作り出す数値の繰り返し精度を数字で表すものだよ!
・生データと平均値、標準偏差、規格上限値と下限値があれば計算できる!
・数字の高い低いだけで単純に良い悪いの判断はできないよ!
いろんな背景を考慮して、自分たちに合った指標にしなきゃいけないよ!
もし、あなたが全く正規分布と工程能力指数を知らなかったならば、正規分布と工程能力指数を使ってデータに基づいて説明するだけで説得力が増します。
知ってても使ってこなかった人は、使えるものには使ってみましょう!
論理的に考えてる感がアピールできますよ(笑)
あなたも正規分パーとして、日々の業務に役立ててくださいね!
おわり


コメント